Typing diary
확장 행렬과 가우스-조던 소거법 본문
2020. 11. 25
행렬은 본래 연립 선형 방정식을 풀기 위해 처음 등장했다고 한다.
확장 행렬과 가우스-조던 소거법은 선형대수학에서 연립 선형 방정식을 푸는 방법 중 하나이다.
확장 행렬
연립 선형 방정식을 행렬로써 표현하는 방법이다.
ex)
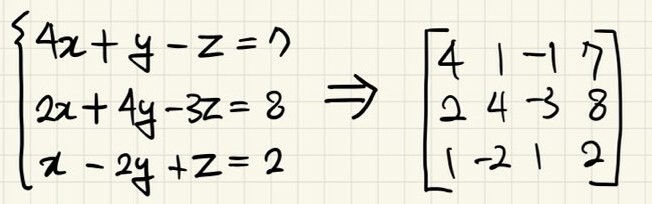
기약행사다리꼴
선행 계수 1이 존재하는 열에서 선행 계수를 제외한 모든 성분이 0인 행렬
아래 행렬들은 모두 기약행사다리꼴이다.

가우스-조던 소거법
행렬을 기약행사다리꼴로 만드는 알고리즘이다.
확장 행렬에 가우스-조던 소거법을 적용해 기약행 사다리꼴을 만듦으로써 연립 선형 방정식의 해를 구할 수 있다.
가우스-조던 소거법은 3가지 기본 연산을 통해 수행된다.
1. 한 행에 상수배를 취한다.
2. 행의 위치를 교환한다.
3. 한 행의 상수배를 다른 행에 더한다.
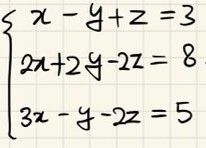
가우스-조던 소거법을 활용하여 위 연립선형방정식을 풀어보자
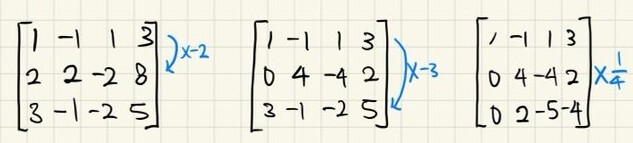
1) 1행에 -2배 하여 2행에 더한다.
2) 1행의 -3배 하여 3행에 더한다.
3) 2행을 1/4배 한다.
이런 식으로 가약행사다리꼴이 될 때까지 진행하면 된다.
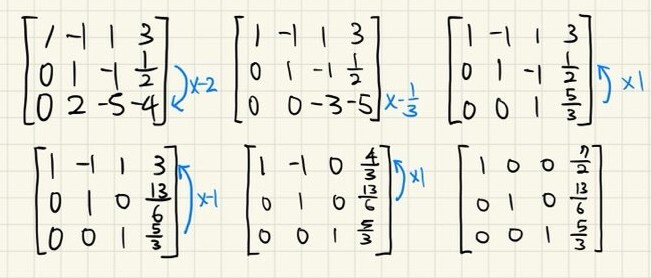
이렇게 구한 해
x = 7/2
y = 13/6
z = 5/3
를 연립선형방정식에 대입해 보면 식이 성립한다는 것을 알 수 있다.
'그래픽스, 게임 수학' 카테고리의 다른 글
| 행렬식(determinant) (0) | 2022.08.21 |
|---|---|
| LU 분해 (0) | 2022.08.21 |
| 벡터 방정식 (0) | 2022.08.21 |
| Dot Product ( 스칼라 곱) (0) | 2022.08.21 |
| 콘솔 창 Double buffering 구현하기 (C++) (0) | 2022.08.21 |




